Hosszú ideje foglalkoztat a kérdés, hogy jól hangolt citerámban a húrok mekkora erővel feszítik a tőkét és a fejet. Ugyancsak kérdéses az is: mi az összefüggés a citerahúrok magyar számozása és a húrméretek között. Ebben a szösszenetben ezeket a kérdéseket járom körül. Közben megadom a Mersenne-Taylor képlet több hasznos formáját és a magyar citerahúr-méret táblázatot. Hátha mást is érdekel, nemcsak a hangszerészeket, akik számára az alábbiak nemigen tartalmaznak újdonságot. Remélem, citerás társaim számára hasznos lesz írásom.

  Most végre van időm és lehetőségem megbecsülni ennek az erőnek a nagyságát. A képletet, amely egy húr első, alapmódusú rezgésének frekvenciáját adja meg, Marin Mersenne (1588-1648) francia szerzetes és matematikus, valamint Brook Taylor (1685-1731) angol matematikus határozta meg. Rendszerint a húr átmérőjét és a húr anyagának sűrűségét felhasználó képletet szokták megadni:

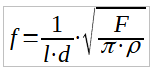 , ahol is:

f: a rezgés frekvenciája Hz=1/s-ban,
l: a rezgő húr hossza m-ben,
d: a húr átmérője m-ben,
F: a húrt feszítő erő N=kg·m/s²-ben,
π: (pi) a Ludolph-féle szám, közelítőleg 3.1415927, és
ρ: (ró) a húr anyagának sűrűsége (térfogategységre vett fajlagos tömege) kg/m³-ben.

A képlet szerint, ha a húr hossza vagy átmérője csökken, akkor a frekvencia, azaz a hagmagasság arányosan nő. Ugyancsak magasabb hangot kapunk, ha a húr feszességét növeljük, de itt a feszítőerőt már négyzetesen – azaz erősebben – kell növelnünk!

(Eszembe jut a múlt évezredből a városi hangszerboltban vásárolt szegedi ládagyári, A tonalitású, azaz E-A citerám. Én, tudatlanul, C tonalitásúra, G-C-re hangoltam fel, a húrokat is vékonyabbra cserélve. Ezt az eljárást ajánlja néhány citeraoktató könyv is. Én nem ajánlom. Abból a citerából hangszer helyett tojásszeletelő lett, annyira felkeményedtek a húrok a túlzott feszítés miatt. Később a nagy feszültség miatt a hangszer érzékelhető módon meghajlott, a sík asztalon bölcsőként billegett és pendítésre kifordult. Megváltam tőle. Nemcsak e miatt, más hibái is voltak.)

Érdekes a ρ szerepe a képletben. A ρ-t, a húr anyagának sűrűségét növelve csökken a frekvencia, de csak gyökösen. Manapság ezért használunk nehézfémmel, pl. rézzel fonott húrokat a bőgőhúrok helyén, egyszerű acélhúrok helyett. A számítást ez nehezebbé teszi, mivel a fonott húr sűrűségét kimérni nehezebb. Alább adni fogok egy módosított (eredetibb?) képletet, amivel ez a nehézség megkerülhető.

Származtatott képletek:

Fejezzük ki az egyes változókat a fenti képletből! Az eredmények:

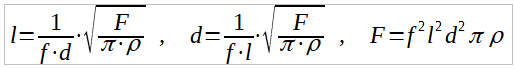
Azaz, pl. a harmadik képletből: a szükséges feszítőerő (és a húr keménysége vagy lazasága) a frekvenciától, a hossztól és a húr átmérőjétől egyaránt négyzetesen, míg a húr sűrűségétől lineárisan függ. Ezért van az, hogy egy átlagosan jó citera csak fél hanggal hangolható lejjebb (egyébként becsörögnek a húrok) és csak egy hanggal hangolható feljebb (a tojásszeletelő-effektus miatt).

A citerahúr átmérője:

A múlt évezred végén (Kádár alatt) a Kozmosz Ipari Szövetkezet “gyártott” – azaz szabott le és csomagolt – különféle nem fonott, acél citerahúrokat. Az átmérőket nem adta meg, a húrokat vastagság szerint számozta. Máig rejtély számomra, mi alapján történt a számozás. Arra tippelek, hogy csak egyszerű katalógus-sorszám volt. Egyik kedves Facebook-ismerős közzétette a méret-táblázatot:

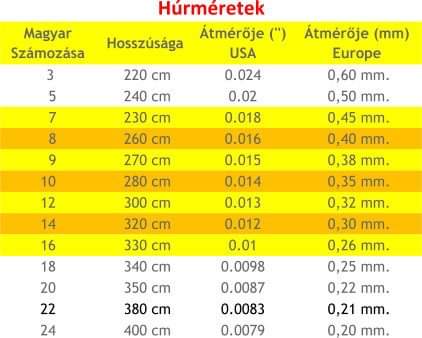
Mérés, adatok:

Nézzük az én citerámat!

A citera három kisfejes, C tonalitású (G-C) tenor, 4+3 db. 7-es dallamhúrral, 1 db. 7-es zúgóhúrral, 1 db. rézzel és 2 db. nikkellel fonott gitár- és basszusgitár bőgőhúrral. Ezen húrok alatt a menzúrahossz egyaránt 707mm. A kisfejeken 2-2-2 db., 7-es húr található, 559mm, 370mm és 257mm menzúrahosszal. (Takarékoskodtam, a citerakészítő ide vékonyabb, 12-es húrokat ajánlott, amelyek a kisebb menzúrahosszon jobban hangolhatóak lennének, de én a maradék 7-es húrokat sajnáltam kidobni.)

A frekvenciák:

• 7-es dallam- és zúgóhúrok: G3, 196.0Hz,

• rézzel fonott gitárhúr, bőgőkórus: C3, 130.8Hz,

• nikkellel fonott basszusgitár húr, bőgőkórus: G2, 98.0Hz,

• drabális, nikkellel fonott basszusgitár húr, bőgőkórus: C2, 65.4Hz,

• első kisfej, 7-es húrok: C4, 261.6Hz,

• 2. kisfej, 7-es húrok: G4, 392.0Hz,

• 3. kisfej, 7-es húrok: C5, 523.3Hz.

A 7-es húrok átmérője (a fenti táblázatból, mivel nincs mikrométerem) 0.45mm. Sűrűségük kérdéses, 7.8-7.85kg/dm³ lehet, számoljunk 7.825kg/dm³-el.

A gitárhúrokkal gond van, mert fonott húrok, átlagos sűrűségükre nincs adat. Róluk később, mert hozzájuk módosított képlet dukál.

Számoljunk!

Egy dallamhúr esetén:

, ami megfelel kb. 95.59/9.81=9.74kg súlyának. Nem kis erő (több, mint 6x1.5l ásványvíz súlya), s ebből az én citerámon kisfejek nélkül 8-szor ennyit adnak a 7-es húrok!

E miatt a feszítőerő miatt kemény a hangszer, viszont jó hangszíne és hangereje van. Ha kényelmesebb hangszert szeretnék, kicsit vékonyabb húrt is választhatnék. 8-ast nemigen kapni, 9-est választva:

Ez már sokkal barátságosabb érték, a hangszer sokkal puhább lenne. Csakhogy erre a méretre történő csere más problémákat okoz. A hangszer 7-es húrokra lett méretezve, azaz a dallamhúrok távolsága a kótaléctől, az érintők helyzete a 7-es húrméretre lett beállítva. Ne felejtsük el ugyanis, hogy a húr lenyomásakor annak feszültsége a húrméret függvényében másként nő, így az érintők helyének is picit változnia kéne húrcsere esetén. Az én citerámon az érintők átmérője nagyobb az átlagosnál, a nyergek is magasabban vannak így azután lágyabb húr esetén a lenyomás erejének változásától a lefogott hang magassága változik, a hangszer nyávog. Így azután a húrcseréről lemondtam. Az ajánlott húrméretnek előnye is van: ebben a beállításban a disszonáns hátsó hang szinte eltűnik: nem tudok akkora ujjnyomást kifejteni, hogy a húr a hátsó érintőn is felfeküdjön, így az ujjam a hátsó hangot erősen tompítja.

A Mersenne-Taylor képlet másik formája

A húrok rezgését leíró egydimenziós_hullám-egyenlet-ben nem a húr anyagának sűrűsége, hanem a húr hosszegységre vonatkozó fajlagos tömege szerepel. A Mersenne-Taylor képlet eddig közölt formája egy kis matematikai trükkel egyszerűen átalakítható erre a formára:

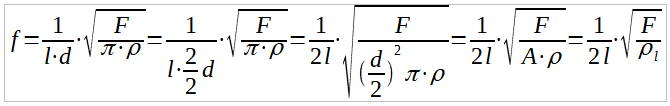
, ahol A a húr keresztmetszetének felülete volt. (Ezzel kiderült, hogy akár ovális húr is használható lenne, csak annak pendítésfüggően más lenne a hangszíne.)

Lényeges, hogy az új képletben ρ_l, az egyszerűbben mérhető hosszegységre vonatkozó fajlagos tömeg (mértékegysége kg/m) szerepel. Ehhez nem kell mikrométer, csak pontos mérleg. Előny, hogy inhomogén (fonott, bevonatos) húrok adata is egyszerűen meghatározható, csak a húr hosszát és tömegét kell lemérni.

Nézzük a képletet még egyszer, származtatott képleteivel együtt:

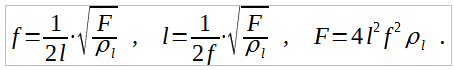
Változók és mértékegységek ugyanazok, ρ_l-t pedig már kitárgyaltuk.

Fonott húr adatok

Megmértem a tartalék húrok hosszát és tömegét. (Sikerült analitikai mérleghez jutnom.) Az eredmények:

• 7-es citerahúr, a) példány: hossza 2.334m, tömege 3.6383g, sűrűsége így: 3.6383/2.334=1.5588x10^-3kg/m.

• 7-es citerahúr, b) példány: hossza 2.342m, tömege 2.5515g, sűrűsége így: 2.5515/2.342=1,08945x10^-3kg/m.

• D Melodia akusztikus gitárhúr: hossza 1.00m, tömege 2.8071g, sűrűsége így: 2.8071/1=2.8071g/m=2.8071x10^-3kg/m.

• D, nikkellel fonott basszusgitár húr: hossza 1.24m, tömege 12.5120g, sűrűsége így: 12.5120/1.24=10.09g/m
  =10.09x10^-3kg/m.

• Drabális, A3, nikkellel fonott basszusgitár húr: hossza 1.05m, tömege 23.2526g, sűrűsége így: 23.2526/1.05=22.145g/m=22.145x10^-3kg/m.

Igen, a 7-es citerahúrokkal probléma van. A b) példány vékonyabb, inkább 9-es lehet, nem 7-es.

...

Kedves olvasóm!

  Félreértés történt. A(z ál)nevem (citerahur) alapján talán azt lehetne gondolni, hogy én netán citerahúrt kívánnék árulni vagy gyártani. Facebook-kalandom során figyelmeztettek: a suszter maradjon a kaptafánál, arról írjon, amihez állítólag ért, a húrokról. Akkor talán többen figyelnének rám.

  Nem kívánom ezt a félreértést tovább fenntartani. Ugyanis nem vagyok más, mint egy mérsékelten öreg, fizikailag beteg citera-bolond. Lélekben az életkorom 18 év – plusz durván 44 év extra élettapasztalat. ;-)

  A névválasztás eredetileg csak szimbolikus akart lenni. Tessék elképzelni a magyar citerás közösséget egyetlen citeraként! Soroljam? Fej, tőke, hangolószegek, nyergek, érintők, káva-részek, stb., le egészen a fedél fájának sejtjeiig, s nem utolsó sorban a legtávolabbi kisfej utolsó húrjáig. Na, egy ilyen húr egy pirinyó darabja vagyok én, lehet, hogy kvinthibás, de még éppen nem döglött. :-)

  Ezt most miért kellett elmagyaráznom?

Kedves citeragyártók, forgalmazók, alkatrész-árusok! Én csak egy fura, citera-használó, elméletieskedő, zeneszerető figura vagyok!

Még mindig írói válságban vagyok, ezért késik a következő rész. A válság lényegét két idézettel világítanám meg. Az első a véleményem, a második a "Párhuzamos történetek" poénja, amit az olvasottsági adatok alapján (érdektelenség? figyelmetlenség?) most lövök le.

Vélemény: "Aki több mondatban mondja el azt, amit egy mondatban is lehet, az egyéb aljasságokra is képes." 

Ezzel a véleménnyel majdnem teljesen egyetértek. Azért csak majdnem, mert szerintem a sommás vélemény alól van kivétel, az igazi író. (Azt, hogy ki az igazi író, nem más, mint az olvasó dönti el. ;-)  Az eddigi statisztika alapján én nem vagyok igazi/divatos? író... )

A poén: "Hangszerünk nem attól magyar, mintha kizárólag csak nálunk fordulna elő, hanem mert nálunk is megtalálható, s néphagyományunk, népzenénk szerves részévé vált. Készítésmódjában, hangolásában, használati módjában sajátos magyar ízlést, igényt tükröz." (Molnár Imre, in: A citeráról mindenkinek, 5. o.)

Tovább is van, írjam még? ....

Nézzük az első penzumot!

Középiskolás koromban (szinte) kötelező tankönyv volt a Kis növényhatározó. Engem ez a segédkönyv teljesen zavarba hozott. Addigra már valamennyire a fejembe verték a Fejlődéselméletet és a Törzsfát. A Kis növényhatározó ezeknek a tudományoknak ellentmondani látszott. Pedig helyénvaló könyvecske volt. Megmutatta nekünk, hogy ha lehetőségek tömkelegével találkozunk ("ez a növény mi lehet?"), nem kell kétségbe esnünk, csak "mindössze" az osztályozás módszeres fegyverével kell  rendet vágnunk a rengetegben. Megmutatta azt is, hogy osztályozási rendszerből nem csak egyetlen üdvözítő (a törzsfa), hanem több alkalmatos is létezik, s használható, használatos. 

Az osztályozási rendszerek többsége döntési fa. A fa minden csomópontjában egy meghatározott döntési kritérium alapján hozunk döntést arról, hogy a csomópontból kiinduló ágak közül melyiket válasszuk, esetünkben melyik hangszercsoport felé haladunk tovább. Ahogy az egymás után következő döntéseket meghozzuk az adott hangszernek az adott kritérium szerinti tulajdonsága alapján, egyre közelebb jutunk a döntési fa adott hangszert képviselő levele felé.

 A XIX. században kezdődött a világ hangszereinek rendszeres gyűjtése. A gyűjteményeket rendszerezni, a hangszereket osztályozni kellett. A legsikeresebb osztályozási rendszert Eric von Hornbostel és Curt Sachs 1914-ben vezette be. A rendszer osztályozási alapelve elsősorban a hang létrehozásának mikéntje, azután a hangszer felépítése és játékmódja. Próbáljuk meg besorolni egy ehhez hasonló a rendszerbe a magyar asztali citerát!

Az első kritérium, mint említettük, a hang keletkezésének módja, azaz, hogy mi kelti a hangot.

• Önmagukban hangzó hangszerek, azaz IDIOFONOK. Ilyenek pl. a bőrhártya nélküli ütőhangszerek, csörgők, stb.
• Rezgő hártya (membrán) kelti a hangot a MEMBRANOFON hangszerek esetében. Pl. az üstdob, és különféle dobok tartoznak ebbe a csoportba.
• Húrral ellátott hangszerek a CHORDOFONok. Igen, a citera ide tartozik.
• AEROFONOK a levegővel megszólaltatott hangszerek, pl. az orgonák, fúvósok, harmonikák.
• Végül ELEKTROFONok az elektromos árammal megszólaló hangszerek.

A következő kritérium lehet a chordofonok esetében a rezonátortest (hangszekrény) és a húr egymáshoz viszonyított helyzete.

• A húr szint közel merőleges a hangszekrényre: hárfafélék.
• A húr szint közel párhuzamos a hangszekrénnyel: citerafélék.

A citerafélék esetében:

• A hangszernek (rezonátor) törzse és azon túlnyúló húrtartó nyaka van: összetett hangszer. (Ide tartozik a lant család és a hegedű család.)
• A húr egyszerű test felett fut, nem nyúlik túl rajta: citeracsalád.

A citeracsalád esetében:

• Fogantyús (nyeles) citerák, pl. botciterák, csőciterák, stb.
• Nyél nélküli citerák.

A nyél nélküli citerák esetében:

• Cimbalomfélék: több húr, a húrok nem rövidíthetők játék közben. Pl.: psalterium, cimbalom, zongora.
• Kombinált citerák: több húr, a húrok vagy egyes (dallam-)húrok a hangszertestre vagy fogólapra helyezett érintőkhöz nyomva vagy nyergekkel vagy érintéssel rövidíthetők, egy húr a rövidítés hatására magasabb hangot ad.

A kombinált citerák esetében:

• Domború citerák: a hangszertest domborított: kin/khin,  kotó, gu-zheng, stb.
• Laposciterák: a hangszertest felső rezonátorlapja lapos. Pl. hasábcitera (scheithold), magyar citera, német koncertcitera, stájercitera, mountain dulcimer, stb.

 Nagyjából meg is érkeztünk. A magyar citera tehát a citerafélék osztályában a lapos dobozciterák érintőkkel ellátott csoportjába tartoznak. A magyar citerának sok hasonló, közeli európai rokona van.

Ez az osztályozás nem pontosan követi az Alasz sorozat Zene kötetét (Urlich Michels: Atlasz, Zene, Athenaum, ISBN: 978 963 9471 20 7), inkább Molnár Imre osztályozása (Molnár Imre: A citeráról mindenkinek, Antológia, 2000. ISBN: 963 7908 94 3, "A húros hangszerek fejlődése és sematikus rendszerezése" c. ábra, 31. o.) mentén halad, de attól is különbözik kissé. Más osztályozási rendszerekkel összehasonlítva látható, hogy minden osztályozási rendszer részben önkényes és szubjektív: az osztályozási rendszert meghatározó kritériumokat és azok alkalmazási sorrendjét az osztályozási rendszer fellállításakor megválasztjuk. 

Mindenesetre látható, hogy a magyar asztali citerának előkelő közeli rokonsága van. ;)

Az alábbiakat a legnehezebb bitekbe kalapálnom. (Én még mechanikus írógépen, majd 110 baud-os elektromechanikus telexgépen tanultam a gépírást, azokat tényleg ütni kellett.) Nem azért, mintha a billentyűzetre kellene annyira vigyáznom. Arra kellene vigyáznom, hogy az igazat írjam a magyar asztali citera eredetéről. Nem fog menni, ugyanis túl sok olyan hipotézis kavarog a fejemben, ami tartalmaz(hat) igazságmagot.

Először egy kis eszmefuttatással kezdem. Két tárgy, pl. egy egyiptomi és egy azték piramis hasonlíthat egymásra hozzávetőleges alakban, s abban is, hogy mindkettő szakrális funkciót töltött be annak idején. Az az állítás azonban, hogy talán az aztékok az egyiptomiaktól tanulták volna a piramisépítést, számomra igen botor elképzelésnek tűnik. Már csak azért is, mert a kétféle piramis kétféle, gyökeresen eltérő funkcióval rendelkezett, eltérő technológiával és belső szerkezettel készült, időben és térben távol egymástól. Meg kell érteni, hogy több, független kultúrában, a kultúrák adott szintjét elérve egymástól függetlenül is kifejlődhet hasonló kultúrtárgy, a kultúráknak nem kell egymástól eltanulnia azok készítési módját, elegendő a hasonló társadalmi-gazdasági szerkezet, amely hasonló igényeket és azok kielégítésére hasonló ötleteket támaszt. Nem feltétlenül igaz az, hogy csak egyszer találnak ki egy új eszközt az "okosabb, fejlettebb" embercsoportok, a többiek pedig csak lemásolnák az új találmányt. Bizony, a fekete lőport, a porcelánt többször is fel lehet találni. (Jó, jó, most ne kezdjünk el azon vitatkozni, hogy Fekete Berthold létezett-e, s kémikus vagy alkimista volt-e valójában. :)  )

 Mindezek ellenére igen gyakori, nagyon valószínűsíthető, hogy egymással bármilyen formában érintkező népek, csoportok, rétegek, kultúrák igenis vesznek át egymástól módszereket, eszközöket, szavakat, kultúrelemeket. Sokszor önként, sokszor kénytelenségből, sokszor kényszerűsítettségből. Mindenesetre nagyon gyakori az, hogy az átvétel nem egyszerű másolással, hanem az átvevő lehetőségei és igényei, kultúrális beágyazottsága által meghatározott módon, átalakítással, a lehetőségekhez idomítással, helyi innovációk bevezetésével történik meg. Sokszor csak az ötletet, az ideát veszik át, az eszközzé fejlesztés már "saját kútfőből" történik. Az átvétel és átalakítás e mellett nem egyszeri alkalom, hanem időben elhúzódó folyamat. A folyamat során az adott eszköz nem behatol, hanem beágyazódik a befogadó/átvevő kultúrába.

Ez történhetett a magyar asztali citerával és az USA-beli hegyi(mountain)/appalachian(epelecsi) dulcimerrel(dulszimerrel) is. Érdekes lesz összevetni a két fejlődési utat és a két hangszerkultúrát, de előtte le kell futnunk egy-két kötelező kört.

Kedves Olvasóm!

 Indíttatva érzem magam arra, hogy bemutassak néhány videót (Forrás: a Youtube). Az első kettő a Tisza '83 citerazenekar 25 éves jubileumi koncertjén készült felvétel. Az elsőn a Klapka-indulót adják elő:

, a másodikon a Tere-fere polkát:

Most pedig következzék valami más, pl. Bing Futch internetes előadása, egy dal, :

(A felvételen nem látszik a lábpedál, amelynek segítségével az előadó az elektronikus kíséretet befolyásolja. forrás: Youtube.)

Ugyan miért is hoztam elő pont ezeket a videókat? Erre a kérdésre fogok válaszolni a későbbiekben, szemérmetlenül hosszú idézetekkel, amelyeket megjegyzéseimmel fűszerezek. 

Amíg következő szösszenetem elkészül, jó kutakodást kívánok hasonló gyöngyszemek után a Világfalu szemétlerakóval kevert intellektuális piacán, az Interneten. 

Mindenekelőtt: nem vagyok történész. Ezért az általam később megjegyzésekkel kiegészített és idézett citeratörténeten kell és lehet is vitatkozni. Azonban mindenképp szükségesnek tartom Molnár Imre munkájának idézését, mivel ilyen mélységű, pontosságú és részletességű történetet a magyar citeráról az Interneten nem találtam, könyvéhez pedig manapság már nem olyan könnyű hozzáférni.

Nem lehet eléggé méltatni Molnár Imre szigetszentmiklósi citerakészítő mester munkásságát. Nemcsak citerái, hanem jelentős citeragyűjteménye is öregbíti hírnevét. A gyűjtemény a szigetszentmiklósi Városi Könyvtár és Közösségi Ház épületében kapott helyet. Ne feledkezzünk meg könyvéről sem, amelyben örökül hagyta ránk a magyar asztali citeráról szóló hatalmas tudásának jelentős részét. A mű minden citera iránt érdeklődő ember polcán ott kellene legyen. 

A mű adatai: Molnár Imre: A citeráról mindenkinek. Kiadta az Antológia kiadó, 2000-ben, Lakiteleken.
ISBN 963 7908 94 3 . 

A kezdetek és az eredet terén még manapság is viták vannak. Molnár Imre  100-120 éves lemaradásról és osztrák-bajor eredetről írt könyvében. Mindenesetre a magyar citeracsalád fejlődésének krónikáját 1850-től kezdi. Ezzel szemben áll egyes körök azon szélsőségesnek tűnő véleménye, miszerint a mai laposciterák elődjét mi magyarok ismertettük volna meg a fejletlen nyugattal már a honfoglalás idején vagy akár azt megelőzően. A hangszer nagyon nagy valószínűséggel ázsiai eredetű ugyan, de a magyar közvetítést én erősen vitatnám. Nehezen tudom ugyanis elképzelni, hogy egy lovasnép laposciterát használna Odo-féle diatonikus érintőkiosztással valamilyen lantszerű húros hangszer helyett. (Lóháton ugyanis igen nehéz lenne citerán játszani, a hangszert asztalra téve vagy térdre és lócára/ágyra/padkára támasztva való megszólaltatni. Azt a képet, amire illusztrációként gondoltam, nem találom ugyan, de helyette itt egy másik, Balogh Sándor 2002-es kiadású Citeraiskolájából, a 96. oldalról:

<< elnézést a képirányokért. Mindegyik kutyaütő szoftveres a maga pártállásától függően forgat képet, így Kedves Olvasóm, kénytelen vagy billegtetni tabletedet, laptopodat vagy mobilodat. Vagy a fejedet. Sajnálom. >>)

Mindenesetre a citera igen ősi hangszer, a kínai régészek pl. kb. 4-5000 éves maradványát találták pár éve. Amit találtak, az egy gu-qin ("ősi kin") hagszertestének töredék darabja volt. Ez az a citera, amelyet a hivatalnok tanoncoknak erősen ajánlott Kung-Fu-Ce (Konfuciusz), tanulás előtti "meditatív bemelegítés" eszközeként. Látható pl. itt: 

 Ez a hangszer a domborúciterák családjába tartozik, most inkább nem foglalkoznék vele. Addig is, míg következő szösszenetem elkészül, jó szórakozva tanulást kíván:

Citerahúr.

Joe Monzo oldalán, a Tonalsoft Encyclopedia-ban, a "dialogus" of Pseudo-Odo címszónál találtam egy érdekes elemzést. A mellett, hogy a Pseudo-Odo tekinthető az egyik első olyan írott emléknek, amelyben az Európában szokásos latinbetűs zenei hang-jelölést (ABCDEFG) használják és magyarázzák, citerások számára is tartogat érdekességet ez az írás. Feltűnő, hogy az Európában elterjedt citerák legtöbbjénél a fogólapon (kótán) ugyanolyan mixolíd hangsor (g-sor: GAHCDEFG... vagy szó-sor: szó-lá-ti-dó-ré-mi-fá-szó...) található, mint amit a Pseudo-Odo is bemutat helyes menzúra osztásként.

Azért, hogy a párhuzam magyar nyelven is érthető legyen, A Pseudo-Odo kérdéses részének fordítását és némi magyarázatot, kiegészítést is közreadnék itt. A fordítás pontosságáért nem vállalnék felelősséget, mivel a latin eredeti angol fordítását fordítottam magyarra.

(Ez a bejegyzés  két angol forrás ötvözéséből származik. Az egyik  Gareth Loy: Musimathics: The Mathematical Foundations of Music (Vol. 2) MIT Press, Cambridge, 2007. ISBN: 978-0-262-12285-6 műve. A másik a HyperPhysics webhely String Wave Equation Development c. lapja.  A fordítást, értelmezést és közzétételt indokolja számomra, hogy hasonló tartalmú és részletességű magyar veblapot nem találtam.)

A hullámegyenletet használhatjuk olyan rezgő testek vagy közegek mozgásának matematikai modellezésére, mint pl. az ideális húr, membrán, vagy a levegő. A hullámegyenlet legegyszerűbb formáját mutatjuk meg. Ebben a formában egydimenziós test, húr modellezhető. (a két dimenziós változattal a membrán, a 3 dimenziós változattal a levegő mozgása lenne modellezhető.) A modellezés során feltesszük, hogy a húr harmonikus mozgást végez, azaz minden egyes részére a rész nyugalmi helyzettől mért távolságával egyenesen arányos nagyságú, a kitérés irányával ellentétes irányú visszatérítő erő hat.

Nem túl fontos, hogy ki vagyok. Azt gondoltam, hogy mindazt, amit a citerahúr kapcsán érdekes, magyar nyelvű megjegyeznivalónak tartok, ebben a blogban gyűjteném és tenném közzé.

Kíváncsi vagyok, mekkora érdeklődésre számíthatok majd.

...