(Ez a bejegyzés  két angol forrás ötvözéséből származik. Az egyik  Gareth Loy: Musimathics: The Mathematical Foundations of Music (Vol. 2) MIT Press, Cambridge, 2007. ISBN: 978-0-262-12285-6 műve. A másik a HyperPhysics webhely String Wave Equation Development c. lapja.  A fordítást, értelmezést és közzétételt indokolja számomra, hogy hasonló tartalmú és részletességű magyar veblapot nem találtam.)

A hullámegyenletet használhatjuk olyan rezgő testek vagy közegek mozgásának matematikai modellezésére, mint pl. az ideális húr, membrán, vagy a levegő. A hullámegyenlet legegyszerűbb formáját mutatjuk meg. Ebben a formában egydimenziós test, húr modellezhető. (a két dimenziós változattal a membrán, a 3 dimenziós változattal a levegő mozgása lenne modellezhető.) A modellezés során feltesszük, hogy a húr harmonikus mozgást végez, azaz minden egyes részére a rész nyugalmi helyzettől mért távolságával egyenesen arányos nagyságú, a kitérés irányával ellentétes irányú visszatérítő erő hat.

Vegyünk két egymást követő képkockát egy képzeletbeli nagysebességű filmről, amelyen egy rezgő húr mozgását vettük fel. A két képkocka felvétele között eltelt időt jelölje Δt. Hogyan jósolhatnánk meg a második kockán látható húr-alakot az első képkocka alapján? Részletesebben, pontosabban: hogyan jósolható meg a húr egy adott, az egyik végétől x távolságra lévő pontjának Δt idő múlva észlelhető y₂ kitérése a kezdeti y₁ kitérésből? Az 1. ábra mutatja a két, egymásra montírozott képzeletbeli képkockát:

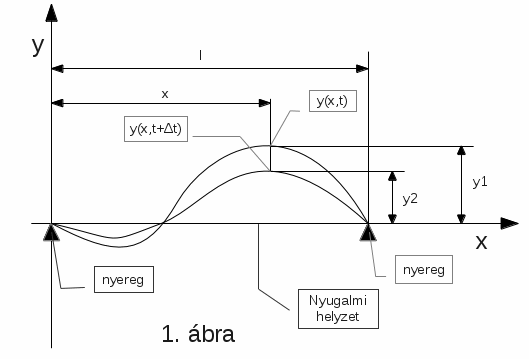
Általánosan: a húr viselkedésének teljes leírásához annak minden x pontja y kitérését meg kellene adnunk minden t időpontban. Azaz (matematikus nyelven) keressük azt az y(x,t) mező-függvényt, amely az (x,t) két dimenziós mező minden egyes pontján megadja az ahhoz a ponthoz (x helyhez és t időponthoz) tartozó y(x,t) kitérést.

Ideális húr

A következő egyszerűsítéseket követjük el a probléma kezelhetősége érdekében:

• A húr legyen homogén, azaz minden egységnyi hosszra eső tömege legyen azonos a húr teljes hosszán,
• A húr legyen teljesen hajlékony, azaz ne legyen szükség semmilyen erőre meghajlításához,
• A húr feszültségéhez (a megfeszítés erejéhez) képest a húrra ható gravitációs erő legyen elhanyagolhatóan kicsiny,
• Csak a húr kicsiny kitéréseit modellezzük. A kitérés és nyúlás legyen elegendően kicsiny minden időpontban. Így ezek nemlineáris hatását elhanyagolhatjuk,
• A valódi húr kétdimenziós transzverzális (le/fel és előre/hátra), valamint longitudinális és torziós rezgésekre is képes. Szorítkozzunk csak a vízszintes rezgés vizsgálatára. Ezzel megmenekülük azoktól a nemlineáris egymásrahatásoktól, amelyek a fenti rezgési módok között felléphetnek azok egyidejű jelenléte esetén.

Az egyszerűsítések ellenére az eredmények jól használhatók lesznek valódi húrok esetében is.

Az ideális húr rezgése

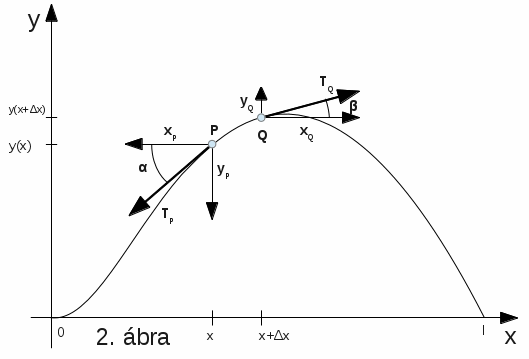
Jelöljük ki az ideális húr egy (kicsiny) darabját a fenti, 2. ábrán szereplő P és Q pontok között. A T_P és T_Q vektorok jelöljék a P és Q pontokban ébredő, a húrszakaszt feszítő erőket. Az ábrázolt pillanatban a P pontot a húr megfeszítéséből származó erő (x_P) húzza balra és a visszatérítő erő (y_P) húzza lefele. Az x_P és y_P komponensek vektoriális összege a T_P. A Q pontban ugyanígy támad a jobbra húzó (x_Q) és felfele kitérítő (y_Q) erő. A két komponens (x_Q és y_Q) eredője (vektoriális összege) a T_Q. Mivel a húrnak modellünkben nincs merevsége (azaz nem áll ellent a hajlításnak), a húrt feszítő erő a húrgörbe érintője lesz a húr minden pontjában, beleértve a P és Q pontokat is. A T_P és T_Q vektorok iránya így a húr pillanatnyi kitérésétől függően változik.

Látható, hogy a P és Q pontokban a húr meredeksége határozza meg T_P és T_Q vektorok vízszintes és függőleges komponenseinek arányát. Az α és a β jelöli a vektorok meredekségét meghatározó szögeket.

Mivel kizártuk a húr-irányú (longitudinális) hullámokat vizsgálódásunkból, ezért az ábrán vízszintes irányú (x_P és x_Q) feszítőerő komponensek egyenlőek és állandóak. Elemi trigonometriával kifejezve:

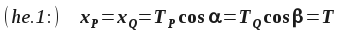
ahol T a húr vízszintes, állandó/változatlan feszítettsége.

Hasonlóan kifejezhetjük a függőleges irányú erőket is. Mivel a T_P lefele mutat ebben a pillanatban, ezért függőleges komponense negatív lesz: y_P = -T_Psinα. T_Q függőleges komponense pedig y_Q = T_Qsinβ lesz. A húrdarabra ható visszatérítő eredő erőt a két függőleges irányú erő irányhelyes (azaz előjeles) összegeként kapjuk:

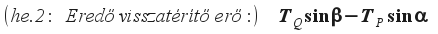
A húrt feszítő erő úgy hat, hogy a visszatérítő erő negatív (lefele mutató) lesz, ha a húrdarab a nyugalmi helyzet fölött van, s pozitív (felfele mutató), ha a nyugalmi helyzet alatt található.

Mivel a húr homogén, a húrdarab tömege a húr hosszegységre eső fajlagos tömegének (ρ) és a húrdarab hosszának (Δx) szorzata lesz. A húrdarab mozgásának leírásához Newton II. törvényét használjuk fel. A törvény egy m tömegű tárgy a gyorsulását adja meg a tárgyra ható f erő függvényében: f=ma . A fentiekben megadtuk a húrdarab tömegét és a húrdarabra ható függőleges irányú erőt, így a húrdarab mozgására felírhatjuk:
f=ma, azaz:

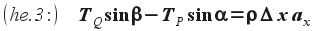
, ahol a_x a húr valamely x pontjának gyorsulása. A (he.3) egyenlet mindkét oldalát osztva a húrt feszítő T erővel:

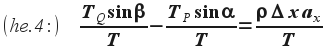Mivel korábban (he.1) már megmutattuk, hogy mindegyik vízszintes irányú erő egyenlő T-vel, ezért tetszésünk szerint helyettesíthetjük azt a (he.4) képletben:

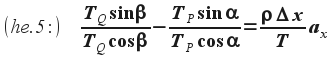Az elemi trigonometriából ismert tanΘ = sinΘ/cosΘ összefüggés felhasználásával (magyarul tg lenne, de a képletszerkesztőm az angol jelölést forszírozta):

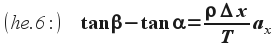Mindkét oldalt Δx-el osztva:

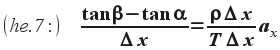
Tudjuk, hogy tanα a húr P pontbeli érintőjének meredeksége, tanβ pedig a Q pontban vett érintőjének meredeksége. A két meredekség különbsége (differenciája) a P és Q közötti húrszakasz átlagos görbülete. Vegyük észre, hogy a (he.7) képlet bal oldala éppen ezen átlagos görbület:

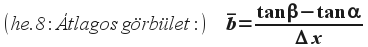
A fenti átlagos görbület definíciót felhasználhatjuk az x pont körüli infinitezimális (pirinyó) szakasz helyi görbületének kifejezésére:

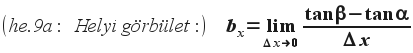Vegyük észre, hogy a tanβ (a húrgörbe érintőjének meredeksége a Q, azaz a húrgörbének az x+Δx helyen vett pontjában) kifejezhető az y(x,t) mezőfüggvény x+Δx helyen vett x szerinti parciális differenciálhányadosával. Ugyanígy a tanα kifejezhető a mezőfüggvény x helyen vett x szerinti parciális differenciálhányadosával:

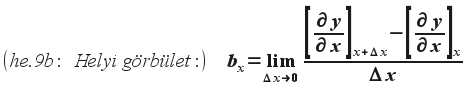, ez pedig láthatóan az y(x,t) mezőfüggvény x helyen vett másodrendű parciális differenciálhányadosa x szerint:

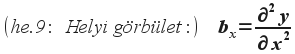Nézzük most a (he.7) egyenlet jobb oldalát! A P és Q közötti húrszakasz tömege a húr hossz szerinti fajlagos tömegének (ρ) és a húrszakasz hosszának (Δx) szorzata. Nem ér minket meglepetésként, hogy a húr egy tetszőleges x pontja körüli infinitezimális (pirinyó) szakaszának tömege éppen a húr hossz szerinti fajlagos tömege (ρ) lesz:

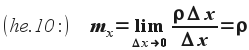
Már csak húr x pontbeli gyorsulásának kifejezése maradt hátra. Tudjuk, hogy az y irányú gyorsulás az út-idő függvény idő szerinti második deriváltja, azaz az y(x,t) mezőfüggvény idő szerinti másodrendű parciális deriváltja:

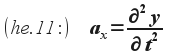Összegezzük az eddig leírtakat! A húr egy x helyen vett b_x helyi görbülete a (he.9) szerinti. Ez a görbület az oka az itteni, (he.10) szerinti m_x tömegű, T feszítés alatt álló húrdarab (he.11) szerinti a_x gyorsulásának. Az összefüggés a (he.7) eddig részletezett infinitezimális átalakításával:

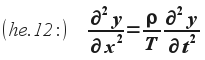
Megérkeztünk, ez az egydimenziós hullámegyenlet, amely egy ideális húr mozgását írja le. Azt még nem tudjuk, hogy a húr egy adott időpillanatban felvett alakja milyen, de tudjuk, hogy az azt leíró mezőfüggvénynek ki kell elégítenie ezt a másodrendű parciális differenciálegyenletet.

Azt is tudjuk, hogy a húr nyergekre ráfeszül, azokon nem mozdul el. Ezért a húr x=0 és x=l "peremein" felírhatjuk az alábbi peremfeltételeket:

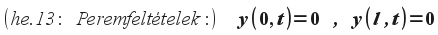
A hullámegyenlet megoldásához már csak a kezdeti állapotot leíró függvényeket, a hullámegyenlet kezdeti feltételeit kell megadnunk. Mivel egyenletünk a pirinyó húrdarabok gyorsulására vonatkozik, ezért nemcsak az y(x,0) kezdeti helyzetet leíró függvényt, hanem a kezdeti sebességet leíró függvényt (a mezőfüggvény t=0 időpontban vett idő szerinti elsőrendű parciális deriváltját) is meg kell adnunk. Ez az a függvény, amely megadja a húr minden pontjának sebességét ebben a kezdeti pillanatban. Ha vizsgálódásunk kezdetének olyan pillanatot választunk, amikor a húr minden pontja "szélső helyzetben van", akkor a kezdeti sebességet leíró függvény értéke minden 0 és l közötti x pontban 0 lesz. (Ilyen pl. az a pillanat, amikor a pengetőt éppen elhagyja a citerahúr.)